Самое актуальное и обсуждаемое
Популярное
Полезные советы

Важно знать!
15 гипоаллергенных смесей для новорожденных — выбираем лучшую
Лучшие молочные смеси для новорожденных – рейтинг, список
«Малютка 1»
В состав входят натуральные компоненты. Смесь содержит 11 микроэлементов, 16 витаминов. Состав сбалансированный и отвечает возрастным...
Читать далее
8 причин геморрагического цистита у женщин: симптомы и лечение
9 факторов которые могут вызвать кашель с кровью
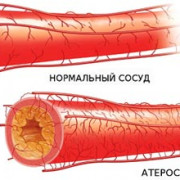
9 привычек для здорового уровня холестерина
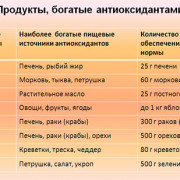
15 продуктов содержащих кальций в большом количестве
12 день после переноса эмбрионов: ощущения, результат, советы медиков, отзывы
4 факта о влиянии пива на кровь человека
2 основных способа лечения тромбоцитопатии у детей
8 причин экстрасистолии сердца по мнению врачей-кардиологов
Пять рок-групп с “убийственными” названиями
Лучшее
Важно знать!
Симптомы и лечение железодефицитной анемии
Диагностика
Когда пациент приходит на прием к доктору, тот вначале узнает, что беспокоит человека, как долго проявляется симптоматика, и какие меры принимались для облегчения состояния. Затем, когда анамнез...
Читать далее
Как подготовиться к флюорографии
Анаприлин: инструкция по применению, отзывы, цена препарата
Применение капотена при давлении (инструкция)
Внезапная тахикардия в состоянии покоя
Признаки инсульта: основные проявления
Все о корвалоле: инструкция по применению, состав в каплях и таблетках
Инструкция по применению таблеток лозартан
Андипал инструкция по применению при каком давлении. андипал: от чего помогает, инструкция по применению при высоком давлении. как влияет андипал на давление
Сахарный диабет
Обсуждаемое
Важно знать!
Инструкция по применению лориста (lorista)
Особые указания
При употреблении на ночь может наблюдаться пробуждение или ночные кошмары, нарушение цикла сна и ухудшение его качества. Связанно это с нарушением функции обратного захвата мелатонина....
Читать далее
Норма сахара в крови у мужчин, женщин по возрасту. Таблица, расшифровка анализа из пальца, вены натощак, при замере глюкометром, через 1 час после еды
Инструкция по применению препарата лозап
Пирацетам (уколы, капсулы, таблетки): инструкция по применению, цена, отзывы, аналоги, рлс, рецепт
От чего помогает кардиомагнил?
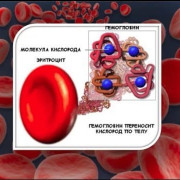
Гемоглобин в крови у женщин: норма, причины колебаний уровня и способы их устранения
Гипертоническая болезнь (гипертония)
Нитроглицерин (nitroglycerin)
Лейкоциты повышены в крови: более 7 причин, лечение лейкоцитоза у ребенка, женщин и мужчин, как снизить уровень
Что делать если болит поджелудочная железа
Популярное
Актуальное

Важно знать!
От чего помогает лоратадин
Рекомендации
Планируя принимать этот медикамент, больные должны учитывать следующие рекомендации:
Лекарство быстро всасывается из желудка.
Активное вещество начинает действовать спустя 15-30 минут после...
Читать далее
Предвестники инфаркта миокарда: симптомы и первые признаки
Анализ крови на коагулограмму
Гипертонический криз: первая помощь, когда тонометр «зашкаливает» (+аудио)
Причины и симптомы энцефалопатии головного мозга
Верапамил (verapamil)
Холестерин
Что показывает анализ крови на тромбоциты?
Как искать в интернете достоверную медицинскую информацию
Синдром всд: тяжелая болезнь здоровых людей
Обновления
 Статьи
Витилиго
Статьи
Витилиго
Симптомы Витилиго:
Витилиго проявляется тем, что на коже больного появляются округлой или овальной...
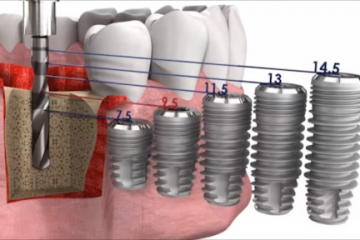 Диагностика
Протетические компоненты и комплектующие для стоматологических имплантатов
Диагностика
Протетические компоненты и комплектующие для стоматологических имплантатов
Как выбрать имплантат?
Как правило, подходящий имплантат выбирает ортопед, ориентируясь на множество...
 Статьи
Реабилитация после коронавирусной инфекции covid-19, сопровождавшейся пневмонией
Статьи
Реабилитация после коронавирусной инфекции covid-19, сопровождавшейся пневмонией
Время восстановления после ковида
Действительно, даже пациенты, перенесшие заболевание в относительно...
Статьи
Удаление бородавок
Бородавка – телу прибавка
Часто папилломы (бородавки) путают с родинками. Бородавки, как и родинки,...
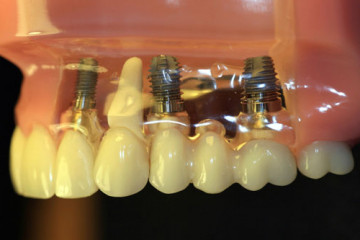 Статьи
Какую имплантацию зубов выбрать: одномоментную или двухэтапную
Статьи
Какую имплантацию зубов выбрать: одномоментную или двухэтапную
Виды имплантации зубов
Все клинические случаи, с которыми сталкиваются стоматологи, индивидуальны....
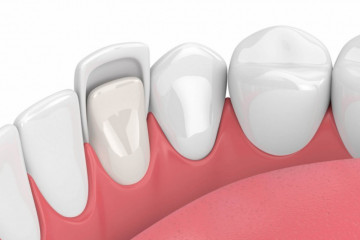 Статьи
Зачем нужны виниры
Статьи
Зачем нужны виниры
Почему керамические виниры лучше композитных?
Многие наши пациенты желают знать: почему в первую очередь...
Статьи
Накрутка зрителей на YouTube и Twitch
Сервисы и программы для накрутки зрителей и подписчиков на Twitch
Можно попытаться заняться накруткой...
Статьи
Наркологическая клиника: эффективное лечение наркозависимых и алкоголиков
Метод Двенадцати шагов
Каждая наркологическая клиника подбирает методики лечения в соответствии со спецификой...
 Что делать при повышенном давлении
Что делать при повышенном давлении
Препараты от давления
Сегодня в аптеках есть много препаратов, которые снижают артериальное давление....
 Диагностика
Что такое брадикардия: основные причины, диагностика и лечение
Диагностика
Что такое брадикардия: основные причины, диагностика и лечение
Диагностика
Правильный диагноз позволит подобрать максимально эффективное лечение.
Чтобы определить...
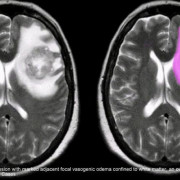
 Почему головной мозг может испытывать кислородное голодание?
Почему головной мозг может испытывать кислородное голодание?
Критерии диагноза
Диагноз внутриутробной гипоксии плода устанавливается на основании таких данных:
Факторы...
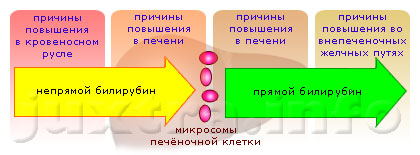 Причины повышения билирубина в крови: чем это опасно и о чем говорит его повышение
Причины повышения билирубина в крови: чем это опасно и о чем говорит его повышение
Причины повышения
Одной из наиболее распространенных причин является гепатит. Он сопровождается отсутствием...